这两天仔细研究了一下SVM的底层数学原理，感觉大学基础数学没好好学，现在看起来真的很吃力啊~~
整理了几篇关于SVM原理的文章，大家有兴趣可以看看。
1. jasper的SVM入门教程，总共有9篇，作者文笔了得，深入浅出，将很复杂抽象的概念都能讲解的特别清楚，非常值得一看。
2.July、pluskid的支持向量机通俗导论（理解SVM的三层境界），讲得十分详细，很多细节都做了推导。
3.勿在浮砂筑高台的【机器学习详解】SVM解二分类,多分类,及后验概率输出以及【机器学习详解】SMO算法剖析
由于编辑公式很繁琐，我在纸上进行了推导。主要参考了勿在浮砂筑高台的推导过程！
在文本分类中有这样一个场景，当我们已经分好词，并构造出词频向量后，这个向量会很大，经常会多达几万维，甚至十几万维。这种规模的模型如果要用SVM等较高级的机器学习进行训练的话，那简直是慢的要死，深度学习就再别谈了。为了较少向量维度，我们可以采用一些方法，比如在词向量中过滤掉词频小于N的词，这个N可以自己定，但一般取值比较小。采用这种方法能有效降低向量维度，但是还是不够。我们不能为了降低向量维度到一定的程度而不断地增大N值，因为这种过滤掉低频次的方法，对向量维度的减少是随着N的增大而逐步降低的，比如说：将N=1，你可以过滤掉10000个单词；接着N=2，你过滤掉了15000个单词；N=3，过滤掉16000个单词；N=4，过滤掉了16800个单词。所以这种方法适用于粗糙地降维。我们可以在原始数据集上利用这种方法先过滤一波词。然后再想别的方法。
那么怎样才能将向量的维度降到我们想要的大小，而不会对整个系统的信息产生重大影响呢？这个问题就是特征选择的问题。
特征选择有2个很明显的优点：
1. 减少特征数量、降维，使模型泛化能力更强，减少过拟合
2. 增强对特征和特征值之间的理解
一般对于文本分类有两种最常用的信息选择方法。一个是卡方检验，另一个是信息增益。但凡是特征选择，总是在将特征的重要程度量化之后再进行选择，而如何量化特征的重要性，就成了各种方法间最大的不同。开方检验中使用特征与类别间的关联性来进行这个量化，关联性越强，特征得分越高，该特征越应该被保留。
在信息增益中，重要性的衡量标准就是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。本文只针对信息增益，卡方检验请自行谷歌度娘。
关于信息增益，大牛Jasper有一篇十分精彩的博文来进行介绍，其计算方法Jasper已经说得十分清楚了。建议你看完这篇文章，再来继续阅读本文。
信息增益最后的推导公式为
我们现在要用python来实现信息增益的计算。
假设我们有4篇文档，每篇文档都已经分好词了：
假设我们词的索引是：
那么我们的文档构造好的词频向量分别是：
假设3篇文档的分类分别是：文档1和文档2属于“0”类，文档3属于“1”类。
那么我们程序的输入就是X，y：
X代表词频向量组成的矩阵
y代表标签向量
我们利用numpy包中的矩阵来包装X，因为它可以提供许多方便的高级函数。
下面就贴上代码，代码里有注释，有兴趣的同学可以好好研究一下，如果你想拿来直接用的话，也是没问题的。代码的效率应该还是可以的，其中有一个比较巧妙的矩阵的转秩。
可以好好理解一下：
以上程序运行结果：
上面的结果代表着
鲜花的信息增益：0.17441604792151594
太阳的信息增益：0.17441604792151594
大象的信息增益：0.17441604792151594
体育的信息增益：0.63651416829481278
乍一看题目，使用”meka“实现分类器，是不是笔者打错了啊，应该是weka啊。其实不然，这世上还真有一个叫meka的包，并且他还跟weka算是亲戚关系。只不过，这个meka是一个专门用来解决多标签分类问题的包，并且是基于weka的，可以算作是weka的一个扩展。
那好，什么是多标签分类呢？我们先来看一个示例：如果我有一篇文章，我要推断它是不是“体育”类新闻，那么分类标签就只有“是”或者“不是”，这种问题就是经典的二分类(binary classifier)问题。好，再复杂一点，如果我们要判断这篇文章是属于“体育”、“财经”、“社会”中的哪一类？那么这个问题就变成了一个多类分类问题(multiclass classifier)，注意，对于每篇文章它只能属于“体育”、“财经”、“社会”中的某一类，不能属于多个类。也就是我们的样本的标签可以是[0,0,1]或者[0,1,0]或者[1,0,0]，但绝不可能是[1,1,0]或者[1,0,1]等。好了，与多分类对应的就是多标签分类(multilabel classifier)，它是解决什么问题的呢？如果一篇文章，它既能属于“体育”类，又能属于“财经类”，甚至还能属于“社会”类，也就是我们待分类的文章有可能同时分到多个类中去，对于这样的分类我们就叫多标签分类。
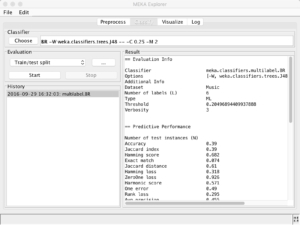
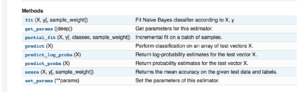
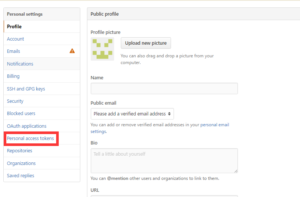
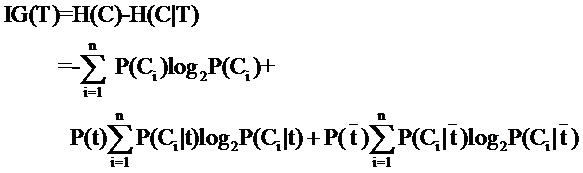明白了多标签分类的概念，我们怎么实现呢？其实说到底，多类分类，多标签分类，其实底层都是二分类组合。我们当然可以自己手动实现。但有没有已有的库来帮助我们实现呢？当然有！！！sklearn中已经有实现多标签分类的方法了，它的底层支持可以是Decision Trees, Random Forests以及Nearest Neighbors. 不过我们这次不使用我们优雅的sklearn，要跳到JAVA的坑去（好桑心）。JAVA中比较有名的多标签分类包是mulan以及meka,我们今天只讲meka，至于mulan的实现方法其实也跟meka很像，甚至在meka中都已经集成了mulan的jar包。
meka是由三个大牛Jesse Read、Peter Reutemann、Joerg Wicker实现，并且现在已经开源到github了，与weka其实是师出同门。meka的使用基本与weka一致，它甚至到包含一个客户端，长相也跟weka很像。
对于图形界面的使用，可以去看看它们的官方教程，很详细。我们今天来说一说如何使用集成meka-1.9.0.jar来进行编程实现。这个jar包存在于lib文件夹下。
meka也是用arff文件作为输入。官方文档中有这么一句话：”A suitable dataset is the only requirement to begin running experiments with Meka.”,足见meka使用之方便~~
meka中已经自带了几个用于实现多标签分类的数据集在data目录下，这个数据集是描述某段音频的特征，以及它们属于哪些分类（是悲伤类的还是安静类的亦或是疯狂摇滚的…）我们来看看大概看看，每行%后面是我自己加的注释：
与weka有点区别的是，对于标签在每个样本集中的位置，weka一般是放在每行末尾，虽然可以放在每行的任意位置，可以通过Instances.setClassIndex(n)方法，来指定每行的第n位是属于分类标签。
先来上代码吧：
输出结果：
甚至还可以使用多标签分类进行增量学习，使用：
meka.classifiers.multilabel.incremental.BRUpdateable类，该类底层使用weka.classifiers.trees.HoeffdingTree来实现。
以前写过一篇博文是利用weka来实现多项式朴素贝叶斯增量学习。这次利用python中的sklearn学习工具来实现。其实个人感觉像机器学习，数据处理这种活本来就应该让我们高雅而优美的Python来实现，Java你瞎凑什么热闹啊~~
与weka的实现相比，sklearn果然还是继承了Python简洁优雅的传统，实现起来十分方便。如何判断sklearn中分类器是否支持增量学习(incremental learning & online learning)呢？很简单，只需要查阅sklearn文档，如果该分类器存在partial_fit()方法，即说明它支持增量学习。
比如我们的多项式朴素贝叶斯中就有该方法：
下面我以一个十分简单的实例来进行演示：
比如我们有三份数据集，先用数据集1进行训练，然后预测数据集3；然后再利用数据集2再对模型进行更新，之后再预测数据集3。
数据集1：‘[ ]’中代表样本向量， ‘#’后面代表样本标签
数据集2：
数据集3（测试集，没有标签）：
代码十分简单，先来看看吧：
运行结果为：(由于数据集是随机生成的，所以每次的结果均会不同)
最终的预测结果表示的是对数据集3中的6个样本，分别预测出的标签。
如果最终需要的结果不是预测出类别，而是需要每个类别精确的概率值。
可以采用方法clf.predict_proba()
GitHub API其实是一座宝藏，它拥有着海量项目以及开发者的各类信息，可以作为社交编程以及经验软件工程课题的数据载体。
本次教程较大家如何使用scrapy来爬取GitHub API，抓取我们所需要的特定信息。GitHub API 是GitHub基于OAuth2协议开放出来的数据获取接口，我们能够在GitHub API上获取各类信息，比如一个项目的commit,issue,pull request;一个用户的粉丝，关注，提交活动，评论等等。GitHub API 有着详细的官方文档教程,上面各类数据的获取接口地址，以及一些过滤参数等。本教程将以爬取rails的issue信息为例，教大家如何使用scrapy来爬取GitHub API。
再开始爬取之前，我们需要进行一些准备工作，由于GitHub API采用OAuth2认证，需要我们提供认证token。当然不提供token可以进行爬取，但是爬取速率会大大降低。
For requests using Basic Authentication or OAuth, you can make up to 5,000 requests per hour. For unauthenticated requests, the rate limit allows you to make up to 60 requests per hour. Unauthenticated requests are associated with your IP address, and not the user making requests. Note that the Search API has custom rate limit rules.
上面显示如果我们提供token可以每小时进行5000次请求，对于非认证(不提供token)一小时只能提供60次的请求，超出请求速率限制后，会返回状态码403 forbidden。有人会问，即使认证后5000次/小时的速率也有些慢啊，如果要更快地进行爬取，那就多注册几个GitHub账号，同时利用多个账号的token进行爬取。GitHub的爬取限制针对的是每个用户，而不是IP，也就是同一台机器，只要你保证每个账号每小时进行小于5000次的爬取，也是完全没有问题的。
接下来我们来展示如何获取自己的token，其实全名为personal access token，每个账号可以拥有多个token，所以不小心哪一天忘了的话，重新生成一个新的即可。
首先我们需要登录自己的GitHub账号。然后在设置里面有一个personal access token选项：
点进去，再点击Generate new token .
选择你想让你的token拥有的权限，一般默认全选即可。点击绿色的Generate token按钮。
这样就生成我们的token了。注意一定要在这时候把token保存下来，这将是你在GitHub上最后一次看见你的token。一旦刷新，token就会隐藏掉。这时候只有生成新的token了。
好了，有了预先的准备工作，接下来就可以编写爬虫了。这次爬虫采用scrapy，关于scrapy相关的知识就不再赘述了，网上有很多教程。
简单说一下爬取思路。
GitHub API 返回的数据都是json，这极大地方便了数据的解析。我们本次的任务是爬取rails项目的所有issue,先来大概看一下返回的issue是什么样子。由于内容太长，我就直接放链接，大家可以点击去看。
https://api.github.com/repos/rails/rails/issues
我们可以看到返回的页面是一个json数组，每个元素其实就是一个issue.而每个issue里面又有诸多信息，比如number,title,body等等。我们本次任务就爬取rails所有issue的信息number，提交者(user.login)，body以及title.
注意，https://api.github.com/repos/rails/rails/issues返回的是按时间倒叙排列的issue,并且每页默认返回30条，我们需要在url后面接上一些参数，来爬取指定的页。我们将url接上参数构造成如下的样子：
https://api.github.com/repos/rails/rails/issues?per_page=99&page=num
其中num代表页数，我们需要从1开始自增。per_page代表每页返回的元素个数,GitHub最大只能制定到99。
所以我们的爬虫，应该是从1开始不停地自增num，直到返回的json数组元素个数不足99，就说明爬取完了。另外，由于GitHub API 爬取速率的限制，我事先准备了10个不同账号的token,对于每次请求，重新自定义请求header,带上不同的token.
下文是源代码：
多元混合效应逻辑回归（Mixed Effects Logistic Regression）是什么：
混合效应逻辑回归是一种二分类模型，其输出是一组预测变量(自变量)的线性组合，但是样本不是简单地独立的，而是集群式分布，也即某个群体之间存在内部关联。
（Mixed effects logistic regression is used to model binary outcome variables, in which the log odds of the outcomes are modeled as a linear combination of the predictor variables when data are clustered or there are both fixed and random effects.）
举个例子：
A large HMO wants to know what patient and physician factors are most related to whether a patient’s lung cancer goes into remission after treatment as part of a larger study of treatment outcomes and quality of life in patients with lunger cancer.
一个医疗机构想要知道对于骨瘤是否最终治愈，医生和病人之间哪种属性是影响最大的。比如医生的属性：从业经验，学历等等。病人的属性有骨瘤大小，患病时间，性别等等。
我们现在就会有一组样本：
我们现在有这组数据，我们现在要预测一个骨瘤病人能否治愈。
普通的多元线性逻辑回归会把每一组样本看成独立的，也就是样本之间是完全独立的，但是实际中我们可以看到，这些样本之间其实是聚集分布的，它们并不是完全独立。同为Bob医生的样本之间肯定存在某种关联，同为Jack医生的样本之间也肯定存在关联。多元混合效应逻辑回归就是加入一个随机效应(上面这个例子中就是doctor),弥补了普通线性回归视样本之间并不存在关联的不足。
混合效应线性回归更加贴近于真实的世界环境。UCLA有十分棒的教程，大家可以去读一读。
那么如何在R里面使用混合效应回归呢？我以混合效应逻辑为例。
读入数据：
对数据中的计数类型（比如年龄啊，从业经验啊等等）进行正规化。为什么需要正规化，请自行谷歌。
引入我们的核心计算包lme4:
进行计算：
输出结果：
有时候我们进行贝叶斯分类时，由于数据量太大导致内存溢出或者对模型的训练有着特殊要求(比如用第一个月的数据预测第二个月，再将第二个月的数据加入已经训练好的模型，去预测第三个月…)，这时普通的贝叶斯分类不行了。我们需要使用贝叶斯来进行增量学习（incremental learning）, weka的贝叶斯分类器即存在增量式的贝叶斯分类器。下文以多项式朴素贝叶斯增量学习为例，weka中的包为：
下文是核心代码：